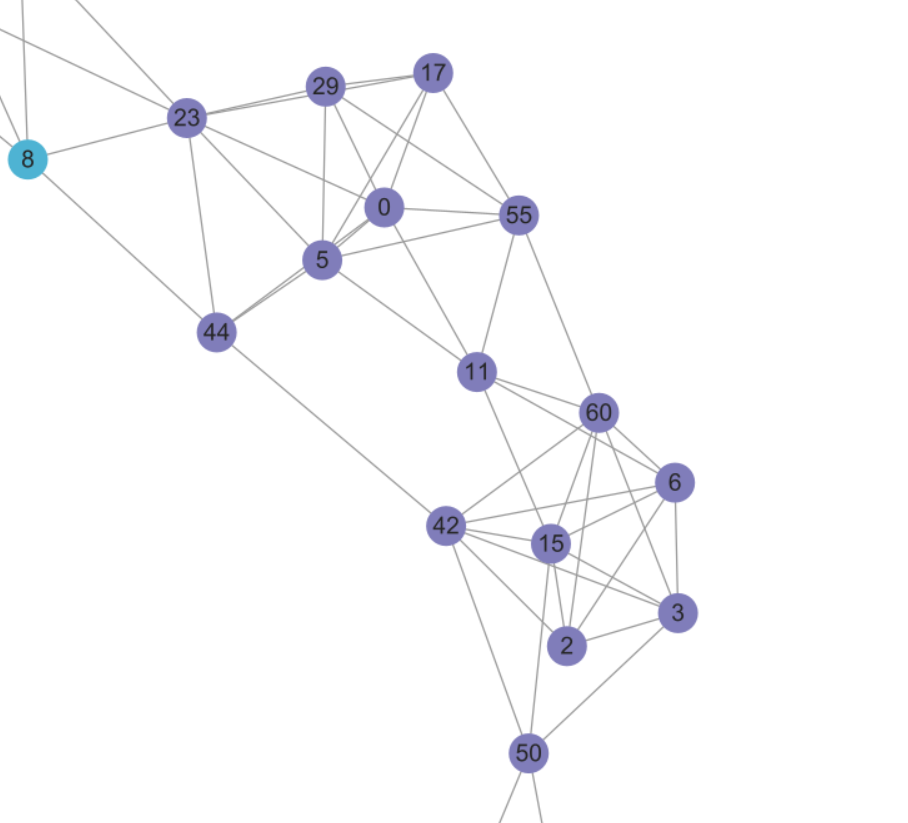
启发式kvcc算法过程可视化
LKVCS过程（以K=4为例）
1.选定一个顶点u=55
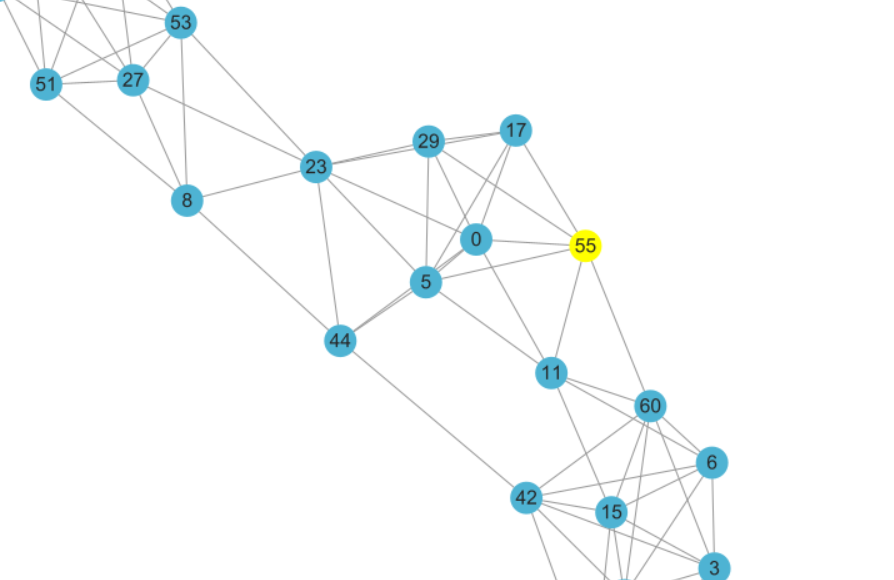
2.获取u的2-hop neighbour记为$N_2(P)$（图中绿色部分）
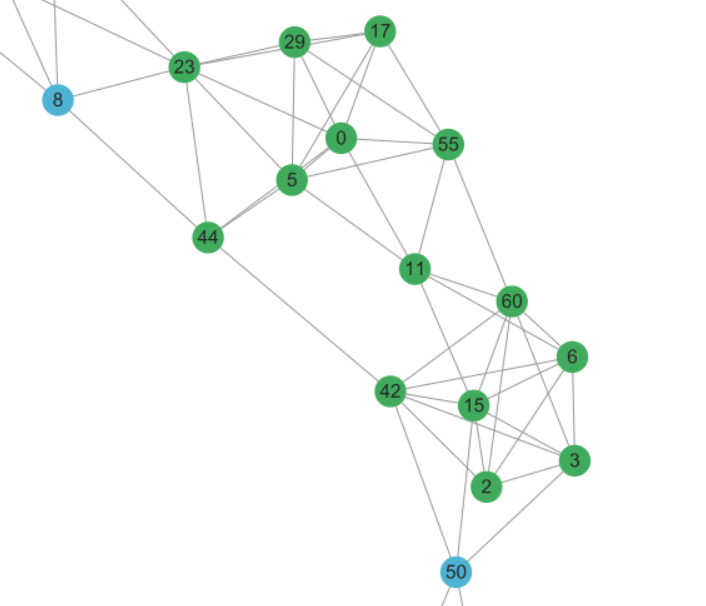
3.获取$N_2(P)$的k-core记为$P^{\prime}$ （图中红色部分）
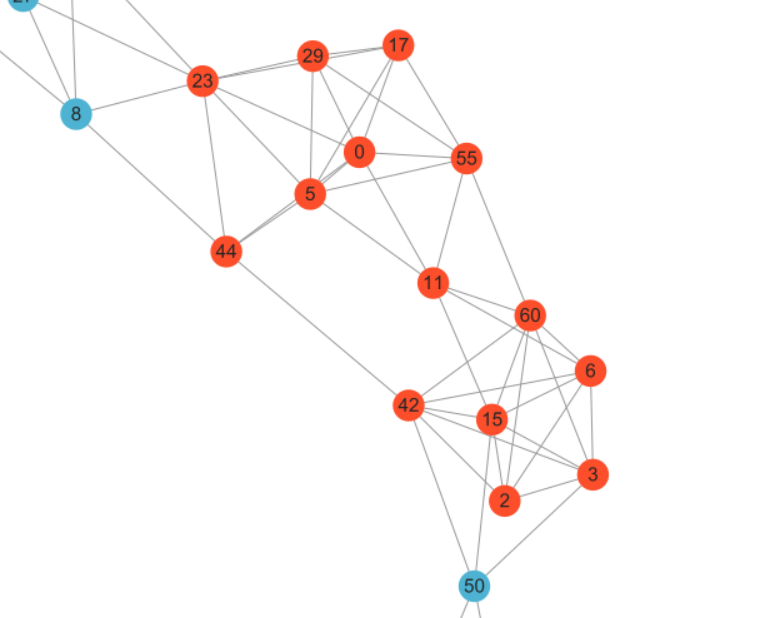
4.获取u在图$P^{\prime}$中的neighbour记为$nb_{G[P^{\prime}]}(u)$ （图中淡紫色部分）
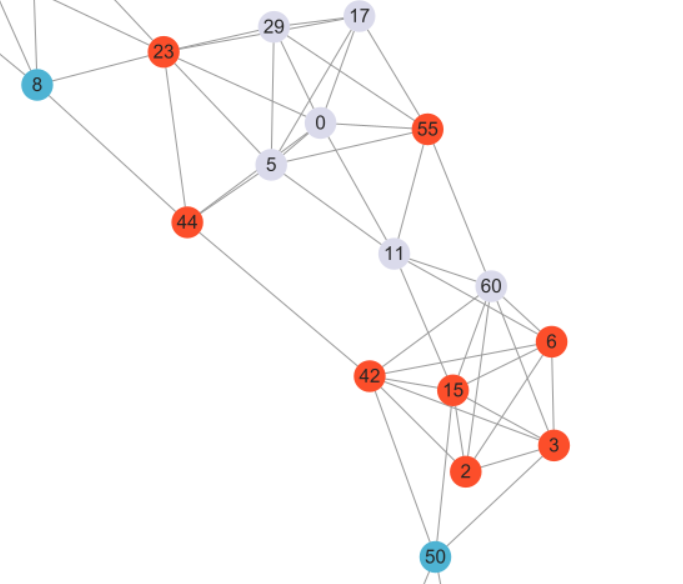
5.从neighbour中得到4个点的组合（k=4）
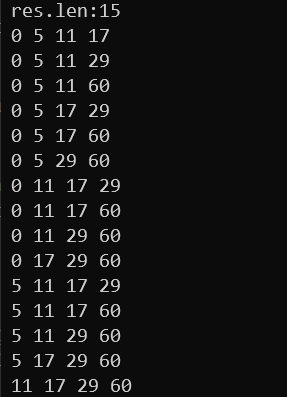
6.从组合中选择一组并将u加入，判断是否可以构建出seed subgraph（图中灰色部分为一个实例）
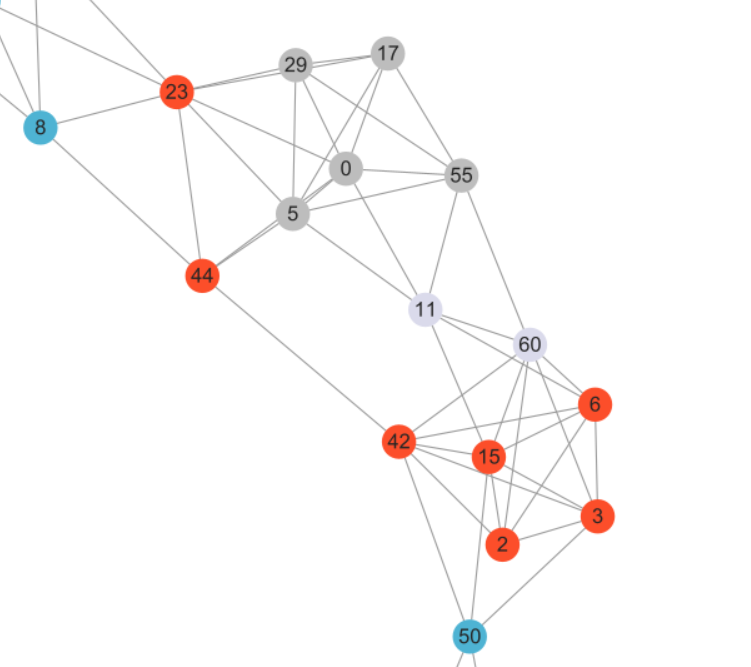
Seeding的全部结果展示
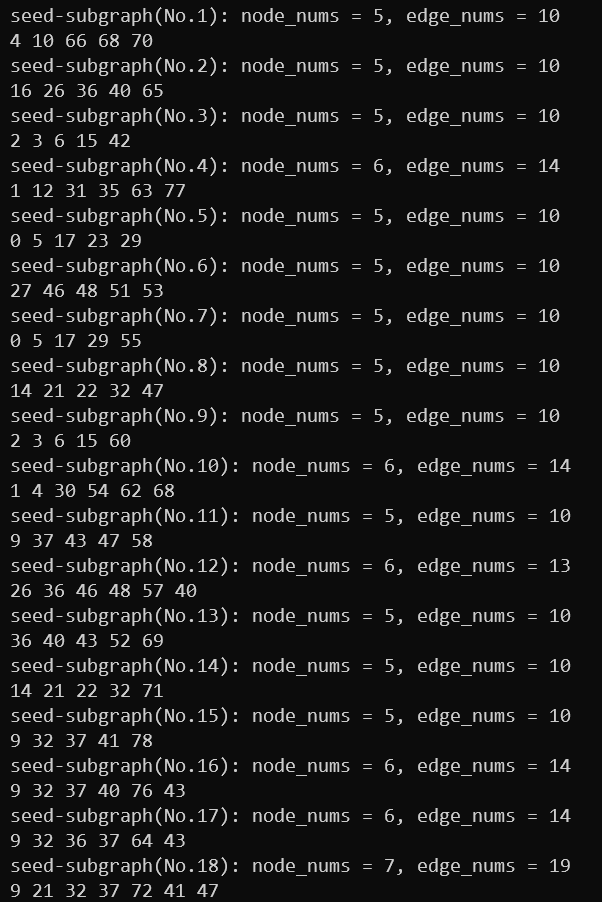
Expanding（以seeding部分得到的seed graph用于演示）
1.确定$\delta \bar{S}$和$\delta S$ （黄色为$\delta \bar{S}$，橙色为$\delta S$）
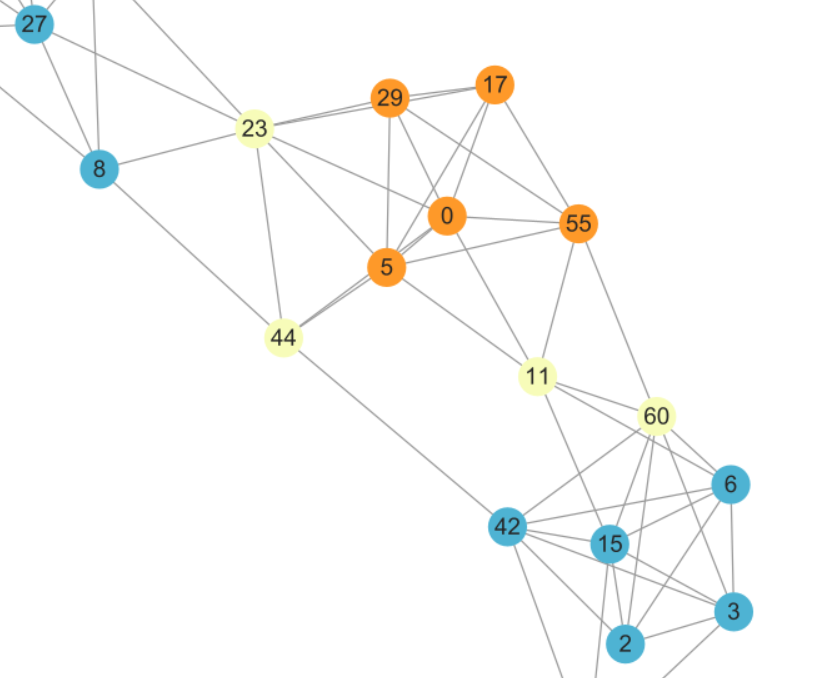
2.从$\delta \bar{S}$不断选取满足$ u \in \delta \bar{S},|n b(u) \cap \delta S| \geq k$的顶点u扩展
发现顶点u=23满足条件，将u=23加入{0 5 17 29 55}
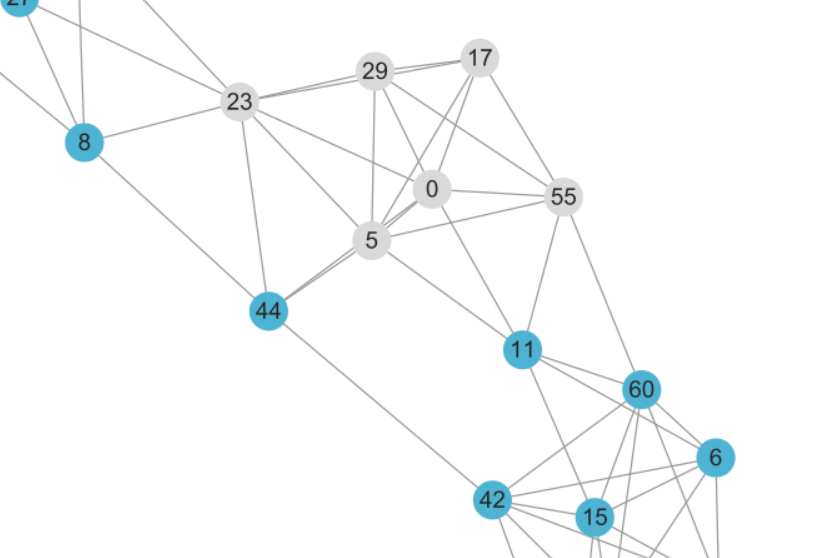
然后返回第一步，重复此过程（下图为更新后结果，黄色为$\delta \bar{S}$，橙色为$\delta S$）
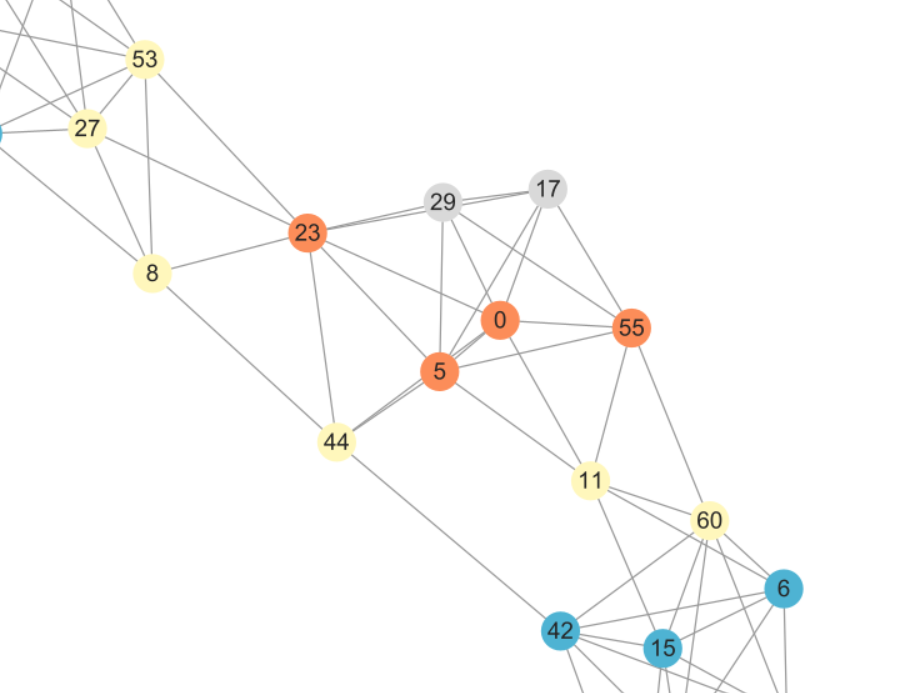
我们发现不存在满足条件的顶点u，终止循环
Merging（因K=4时没有用到merging操作，故以K=5为例）
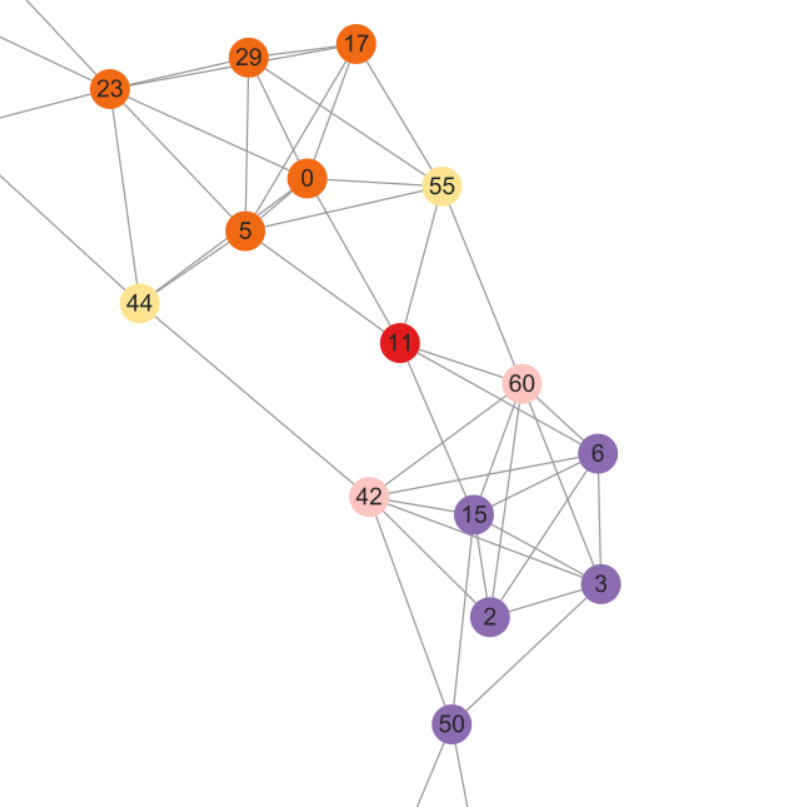
通过之前的seeding和expanding操作更新种子子图，从中取两个为一组进行判断是否可以合并，以下为一组可以合并的实例。 {0 5 11 17 23 29 44 55}表示为$S$， {2 3 6 11 15 42 50 60}表示为$S^{\prime}$，重叠顶点编号为11
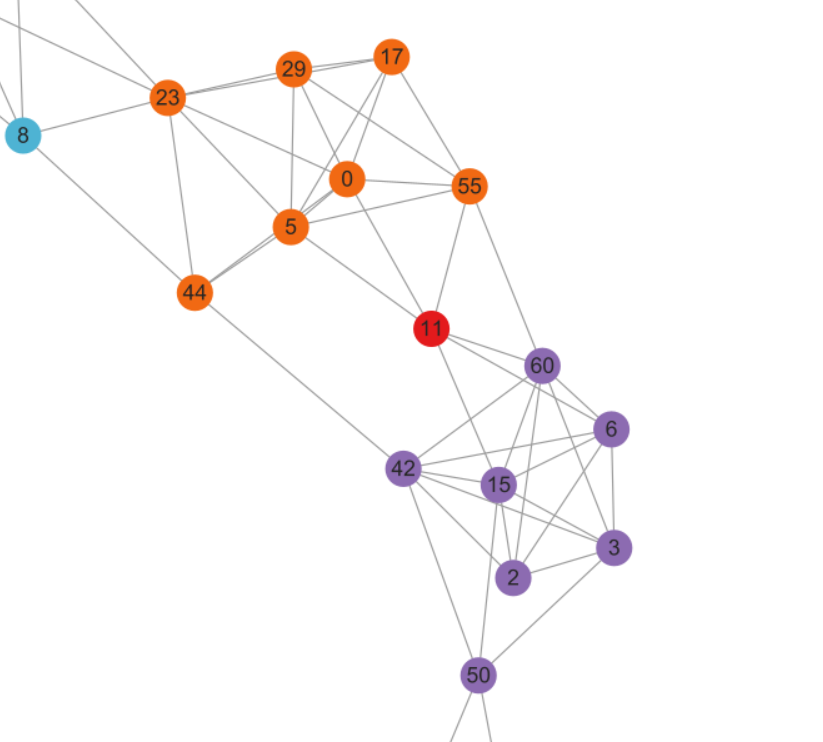$\left|n b_{S \backslash S^{\prime}}\left(S^{\prime} \backslash S\right)\right|$ 为黄色, $\left|n b_{S^{\prime} \backslash S}\left(S \backslash S^{\prime}\right)\right|$ 为粉色,
则 $\left|S \cap S^{\prime}\right|+\min \left(\left|n b_{S \backslash S^{\prime}}\left(S^{\prime} \backslash S\right)\right|,\left|n b_{S^{\prime} \backslash S}\left(S \backslash S^{\prime}\right)\right|\right)=1+\min (2,2)=1+2=3 \geq 3$, 所以合并两个社区
得到{0 2 3 5 6 11 15 17 23 29 42 44 50 55 60}
